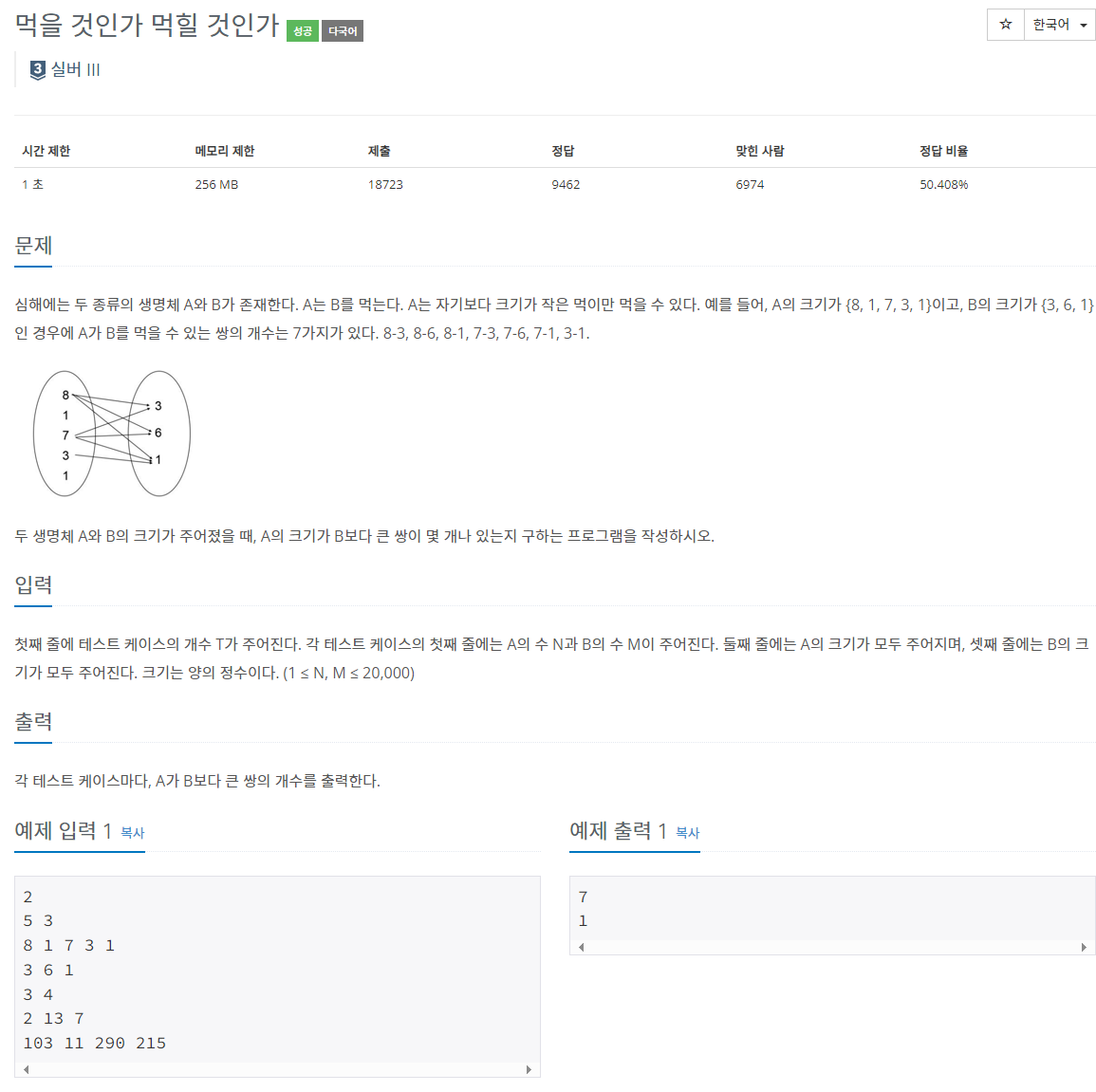
아래는 문제와 링크입니다.
코드를 먼저 보고 이 문제에서 얻어갈 점을 확인해 보겠습니다.
from bisect import bisect_left
T = int(input())
for _ in range(T):
N, M = map(int, input().split())
A = sorted(map(int, input().split()))
B = sorted(map(int, input().split()))
count = sum(bisect_left(B, a) for a in A)
print(count)
1. **이진 탐색의 활용**: 정렬된 배열에서 특정 값보다 작은 원소의 개수를 세는 데 이진 탐색을 사용할 수 있다는 걸 알 수 있습니다. 이건 아주 중요한 테크닉입니다.
count = sum(bisect_left(B, a) for a in A)이 부분에서 `bisect_left` 함수를 사용해 이진 탐색을 구현했습니다. 이 함수는 B라는 배열에 a를 삽입할 수 있는 가장 왼쪽 인덱스를 반환합니다. 즉, B에서 a보다 작은 원소의 개수와 같습니다.
# 참고로 bisect 모듈은 내부적으로 이진 탐색 알고리즘을 구현하고 있습니다.
2. **bisect 모듈의 유용성**: Python의 bisect 모듈이 이진 탐색을 얼마나 쉽게 구현할 수 있게 해 주는지 알 수 있습니다. 이런 내장 모듈을 잘 활용하면 코드를 효율적으로 작성할 수 있습니다.
from bisect import bisect_left
이렇게 bisect 모듈을 임포트 해서 사용하여 이진 탐색 알고리즘을 직접 구현하지 않았습니다.
3. **시간 복잡도 개선**: 단순한 이중 반복문을 사용하는 대신 이진 탐색을 사용함으로써 시간 복잡도를 O(NM)에서 O(NlogM)으로 줄일 수 있습니다.
count = sum(bisect_left(B, a) for a in A)
이 부분에서 A의 각 원소에 대해 B에서 이진 탐색을 수행합니다. 이렇게 하면 시간 복잡도가 O(N log M)이 돼서 효율적으로 문제를 해결할 수 있어.
4. **입력 처리와 정렬의 동시 수행**: `sorted(map(int, input().split()))`와 같은 방식으로 입력과 정렬을 한 번에 처리하는 방법을 알 수 있습니다.
A = sorted(map(int, input().split()))
B = sorted(map(int, input().split()))
이런 방식으로 코드를 더 간결하고 효율적으로 만들 수 있습니다.

'백준 문제풀이' 카테고리의 다른 글
| [백준] 32930번 슈팅 연습 - Python(1편) (1) | 2024.12.20 |
|---|---|
| [백준] 2231번 분해합 - Python(1편) (0) | 2024.12.18 |
| [백준] 20920번 영단어 암기는 외로워 - Python(1편) (1) | 2024.12.15 |
| [백준] 1449번 수리공 항승 - Python(1편) (0) | 2024.12.14 |
| [백준] 11652번 카드 - Python(1편) (2) | 2024.12.13 |



